Текст всей главы с подробным описанием метода характеристической полосы Хорна находится по ссылке http://uic.nnov.ru/~egyb/doc/horn11_4.zip
Здесь представлена середина 11 главы из книги Хорн Б. К. П. "Зрение роботов" Пер. с англ. — М, Мир, — 1989.
(скачать текст книги можно в формате MS Word .doc на uic.unn.ru/~egyb/lit.html или в формате .djvu на padabum.com/d.php?id=4144)

Коротко о Методе характеристической полосы (методе Хорна по распознаванию формы на изображении):

11.1.4. Общий случай

Предположим, что мы имеем координаты некоторой точки поверхности и хотим продолжить решение из этой точки. Используя малое

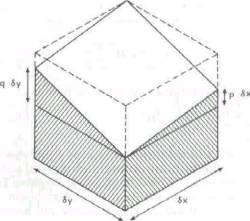
Рис. 11.4. Изменение высоты δz как сумма изменений высот рδх и qδy, обусловленных малым шагом по x и y соответственно.

приращение (δx,δу), мы ещё раз заметим, что изменение дальности (или глубины) задается выражением δz = р δх + q δу, где р и q — первые частные производные z по x и у (рис. 11.4). Больше ничего нельзя сказать, пока не станут известны р и q. К сожалению, уравнение освещённости изображения даёт только одно условие; этой информации недостаточно, чтобы получить решение как для р, так и для q.

     Предположим временно, что мы узнали р и q в данной точке. Тогда мы можем продолжить решение из точки (x, у) в точку (x + δx, y + δy). Однако для этого необходимы новые значения р и q в этой точке (рис. 11.5). Теперь изменения p и q можно вычислить по формулам δp = r δx + sδy и δq = sδx + tδy, где r, s и t — вторые частные производные по z, х и у. Их можно переписать в компактной форме

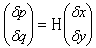
где Н — матрица Гессе вторых частных производных (гессиан)

H =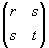

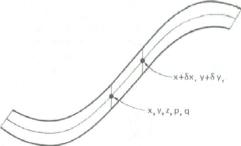
Рис. 11.5. Решение задачи восстановления формы по распределению полутонов, определяемое решением пяти дифференциальных уравнений относительно х, у, z, р и q.

Результатом является характеристическая полоса, т. е. кривая в пространстве, вдоль которой известна ориентация поверхности

Матрица Гессе дает информацию о кривизне поверхности. Для малых наклонов поверхности её детерминант является гауссовой кривизной, которую мы введём ниже. Кроме того, след матрицы Гессе (сумма её диагональных элементов) — это лапласиан дальности, который для малых наклонов поверхности равен удвоенной так называемой средней кривизне. Мы будем изучать кривизну поверхности в гл. 16 при рассмотрении расширенных гауссовых образов.

При использовании матрицы Гессе для вычисления изменений р и q необходимо знать её компоненты (вторые частные производные z). Чтобы следить и за ними, нужно знать производные более высоких порядков. Так можно было бы продолжать дифференцирование до бесконечности. Однако заметим, что мы ещё не использовали уравнение освещённости изображения. Дифференцируя его по х и у и используя правило дифференцирования сложной функции, получим E_x= r·R_p + s·R_q и E_y = s·R_p + t·R_q или

, где снова появляется матрица Гессе Н. Это соотношение связывает градиенты на изображении (Е_x, Е_y)^T и на карте отражательной способности (R_p, R_q)^T. Мы не можем разрешить его относительно Н, поскольку имеем только два уравнения и три неизвестных r, s и t, однако, к счастью, нам не нужно знать отдельных элементов матрицы Н. Ведь мы не можем продолжать решение в произвольном направлении, а только в некотором специально выбранном направлении. В этом ключевая идея подхода. Положим где δξ — малая величина. Тогда

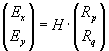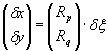
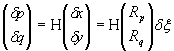 или

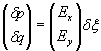
     Таким образом, если направление смещения на плоскости изображения параллельно градиенту на карте отражательной способности, то можно вычислить изменения (р, q). В свою очередь направление смещения в градиентном пространстве параллельно градиенту на изображении (рис. 11.6). Мы можем подытожить всё это в виде пяти обыкновенных дифференциальных уравнений
x′_ξ = R_p,
y′_ξ = R_q,
z′_ξ = p R_p + q R_q,
p′_ξ = E_x,
q′_ξ = E_y,
где штрихи означают дифференцирование по ξ. Решение системы этих уравнений является кривой на поверхности. Вдоль неё будет изменяться параметр x. Масштабированием этих уравнений мы можем сделать параметр x любой функцией длины кривой.

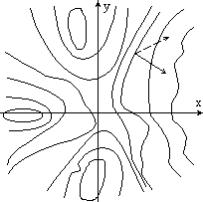
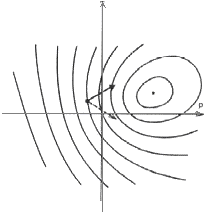
Рис. 11.6. Шаги, взятые в пространстве градиентов рq и пространстве изображения xy, параллельны градиентам Е(х, у) и R(p,q) соответственно.

11.2. Характеристические и начальные линии

Кривые, являющиеся решениями пяти обыкновенных дифферен­циальных уравнений  называются характеристическими линиями, а их проекции на изображение — базовыми характеристиками. В действи­тельности решения для x, y, z, р и q образуют характеристическую полосу, так как они определяют не только кривую в пространстве, но и ориентацию поверхности вдоль этой кривой (рис. 11.5).

Для получения полной поверхности мы должны «сшить» характеристические полюсы. Каждая из них должна иметь точку, в которой заданы начальные значения; из нее начинается решение. Если нам задана начальная линия на поверхности, то решение для поверхности можно

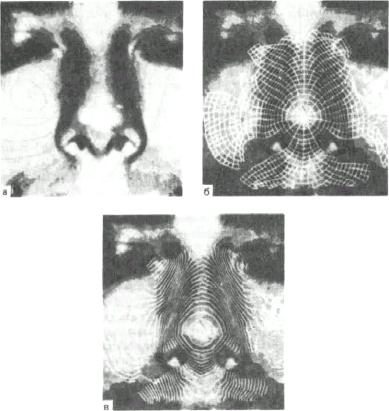
Рис. 11.7. Метод восстановления формы по распределению полутонов исполь­зуемый для восстановления формы носа.

а — грубо дискретизированное полутоновое изображение, готовое к вводу в компьютер; б — базовые характеристики, наложенные на первое изображение; в — линии уровня, вычисленные по оценкам, найденным вдоль характеристических кривых.

получить, если эта линия нигде не касается ни одной из характеристик. На этой линии начальные величины р и q можно получить с помощью уравнения освещённости изображения Е(х, у) = R(р, q) и известных производных z вдоль кривой, Предположим, например, что начальная линия задана через параметр h в виде x(h),  у(h) и z(h). Тогда вдоль этой кривой  ∂z/∂η = p (∂z/∂η) + q (∂y/∂η).

Мы сейчас ввели метод распространения характеристической полосы при решении дифференциальных уравнений в частных производных первого порядка. В нашем случае релевантным уравнением является уравнение освещённости изображения, т. е. (возможно, нелинейное) уравнение в частных производных первого порядка. На рис. 11.7 представлены изображение лица, преобразованное в цифровую форму, то же лицо с наложенными на него базовыми характеристиками и то же лицо с линиями уровня восстановленной поверхности.